BTC White Paper解讀

比特幣主要想解決透過網路點對點之間直接的交易, 而不透過第三方公正單位的介入
傳統金融其實對我們生活上面其實已經很方便了, 例如想領錢就領錢, 想匯款也馬上可以匯款成功
那麼比特幣到底想改變甚麼呢?

比特幣認為傳統金融需要第三方公正單位導致成本上升

比特幣認為傳統金融無法做到 completely non-reversible transactions (完全無法回復的交易)
因為傳統金融不能避免調解糾紛 (不確定是因為銀行的運作模式不能, 還是因為社會不允許銀行不做這件事), 然而因為調解糾紛需要成本, 所以這些成本都加諸在了交易上面, 間接導致了很多微小金額交易的可能性 (然而現在看起來加密貨幣更是沒有做到這一點), 但比特幣認為更大的成本是在於無法做到 non-reversible transactions for non-reversible services, 由於有reversal交易的可能性, 商人會擔心他們的客戶, 所以常常會索要更多客戶的資訊(超出他們所需要的)

比特幣認為這世界存在著一定詐騙的行為, 當人們面交時直接交互實際貨幣, 就不會遇到這種問題 (其實還是有假幣的可能性?), 但使用電子通道交易的時候就不能不加入第三方公正單位

比特幣如何做到

比特幣認為應該使用一種電子加密證明機制來取代所謂的信任機制, 透過無法逆轉交易將可以保護賣家免受詐欺, 而可以透過常規的託管機制來保護買家

然而要做到完全無法reverse交易, 必須要解決雙花問題(double spending), 這篇paper主要就是要解決這個問題

In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions

比特幣的交易機制(避免雙花機制)

電子貨幣利用電子簽名來達成交易
define an electronic coin as a chain of digital signatures

可以想像成有一個錢幣, 在Owner 1手上, 如果Owner 1要將幣轉給Owner 2, Owner 1將這個幣加上自己的Public Key做hash, 形成Owner 1將這個幣交給Owner 2的證明

然而這無法證明Owner 1不會進行雙花的行為, 最常見的作法是每筆交易必須回到一個受信任的中央機構, 每當交易結束後, 中央機構會回收幣, 並且鑄造(mint)新的幣, 並且使用者只能使用這些新的幣做接下來的交易, 等於任何交易都必須透過這個中央機構的介入才能確保安全

對於比特幣來說, 認為先到的交易就是真的, 後到的就該捨棄, 所以唯一的問題就變成了, 如何確認哪筆交易先到?, 在上面的作法是, 中央機構會知道所有的交易, 並且決定哪個交易先到哪個交易後到, 而對於比特幣來說則是所有的參與者必須同意一份唯一的帳本歷史, 交易要成功必須讓大部分的節點都同意這筆交易是先到的

由於不希望有第三方公正單位的介入, 所以所有的交易都是大眾可見的

Timestamp Server

首先需要建立一個Timestamp Server, 只是這裡的Timestamp是利用hash來代替, 將一堆item打包成一個Block, 並且根據這些資料形成的Hash作為Timestamp, 這樣可以確保該筆交易是在該Block發生, 而每個Hash除了根據Block的資料, 還包含了前一次的Timestamp, 形成一條chain

Proof-of-Work

為了實現distributed timestamp server on a peer-to-peer basis, 還需要proof-of-work

我們可以根據hash算法出來的結果的前幾位數有幾個0作為Proof-of-Work, 為了實現Proof-of-Work, 比特幣在block裡面加上一個Nonce, miner必須找到適當的Nonce使得該hash滿足前幾位數為0來作為proof, 並且後面的鏈也是跟著先前的鏈完成的, 所以鏈越長, 越能確保該block是正確無誤的

這樣的方式還可以解決多數決作弊的問題, 如果根據每個IP有一票來投票, 那麼任何人都可以生出很多的IP作為攻擊者, Proof-of-Work就是依照CPU算力來當投票 (其實就是利用CPU的成本當作稀缺資源), 並且總是選擇最長鏈(因為上面具有最大的Proof-of-Work), 只要大部分礦工是誠實的, 那麼attacker就沒有辦法攻擊, 因為網路會選擇誠實礦工的最長鏈, 為了滿足差不多的交易速度, 因此只要鏈上的生成數量太快, 那麼區塊鏈難度就會增加, 反之, 則會減少難度

Network

1. 新交易廣播到全部的節點(nodes)
2. 每個節點收集交易打包成block
3. 每個節點計算nonce去找到proof-of-work for this block
4. 一旦找到了proof-of-work, 就廣播給其他節點
5. 節點驗證該區塊的交易是否都有效
6. 節點會幫忙散播此區塊, 因為他們想要創建下一個區塊也是根據此區塊創建的, 所以必須幫助此鏈獲得最長鏈

Incentive

做為激勵參與者進行驗證, 比特幣將會給予第一個包裝好區塊的人比特幣作為獎勵, 同時這也是發行此貨幣的唯一一個方式
穩定的增加黃金並發行貨幣, 只是在比特幣的例子中, 是使用CPU算力跟時間作為resources
透過激勵, 可以鼓勵礦工誠實, 因為礦工如果有算力破壞比特幣鏈上數據的真實性, 以獲得雙花的情況, 那麼不如乖乖遵守規則, 賺取對應的工資

Reclaiming Disk Space

一旦交易已經經過了後面幾個block的確保正確性後, 這個交易就可以基本上就可以丟棄節省空間

把每一筆交易兩兩hash起來, 迭代的形成一個Root Hash放到區塊當中, 這樣區塊就不需要儲存大量的交易資料, 需要做驗證的時候跟Full node索要該區塊的Merkel Tree進行驗證, 即可證明該筆交易確實在該區塊當中(如右圖), 對於使用者可以很輕鬆地加入到比特幣區塊鏈當中使用比特幣, 而不會造成太高的門檻

Full node

Full node即儲存所有交易訊息的節點, 比特幣建議的full node的規格如下

• 200GB的儲存空間, 讀寫速度要在100MB以上
• 2GB以上的記憶體
• 上傳速度400Kbps的網路

如果要把所有交易資訊存在Full node那麼需要200GB, 然而一般的驗證者(使用者)並不需要儲存Full node的交易資訊

SPV(Simplified Payment Verification) node

透過Merkel Tree的幫助, User可以只安裝SPV node, 裡面只有每個Block的header
透過Merkle Tree要去檢查某個交易是否存在某個區塊中, 就去訪問Full node並且索取該區塊的Merkel Tree進行驗證, 這樣一年只需要增加4.2MB的資料, 使得大家都可以輕鬆地使用比特幣區塊鏈

這邊也會導致Overpower的節點可以產生攻擊, 一旦使用者發現有invalid block, 就需要去下載full block做驗證, 通常企業最好運行自己的節點, 一來驗證的速度比較快, 二來具有獨立的安全性(確保自己手上的full block是正確的)

Combining and Splitting Value

雖然製造coin來交易不是甚麼難事, 但是因為交易總是會有cent等更小的單位需要切割, 所以比特幣採用input, output的方式來記錄帳

Privacy

比特幣利用public key做交易, 所以沒有人可以連結回去這筆交易是誰做的
比特幣認為這跟股票交易很像, 大家丟出來股票跟錢做搓合, 卻沒有人知道哪張股票是誰的
雖然不知道詳細是誰在做交易, 不過卻可以知道特定的人做了特定的行為, 也就是鏈上的鯨魚是可以追蹤的

Calculations

即使attacker真的比honest還快, 但是他們這也不代表他們可以任意竄改鏈上數據, 例如他們不可能無中生有, 因為其他節點不會接受憑空出現的帳, attacker頂多只能拿回他們最近交易的錢

由於我們知道, 攻擊者或者鏈上有可能分岔, 但比特幣會採用最長的那條鏈而弭平這些分歧, 且交易的時候receiver才會將自己的public key發出來, 使得attacker沒有辦法提前作弊, 那麼我們想知道的是交易發出後多久, 這個區塊鏈上的交易才可以被確保是安全的?

Poisson Distribution

在介紹比特幣計算之前先介紹一下Poisson Distribution

如果不想深究數學的話可以跳過這一小段計算, 可以只看最後Poisson Distribution的最後推導結果

考慮以下幾種現象：每小時服務台訪客的人數，每天家中電話的通數，一本書中每頁的錯字數，某條道路上每月發生車禍的次數，生產線上的疵品數，學生到辦公室找老師的次數……。大致上都有一些共同的特徵：在某時間區段內，平均會發生若干次「事件」，但是有時候很少，有時又異常地多，因此事件發生的次數是一個隨機變數，它所對應的機率函數稱為 Poisson 分配。

一個 Poisson 過程有三個基本特性：

(1) 在一個短時間區間 $\Delta t$ 內，發生一次事件的機率與 $\Delta t$ 成正比： $\lambda \Delta t$。(代表$\Delta t \lambda$為均值得概念)
(2) 在短時間內發生兩次以上的機率可以忽略。(可以想成機率函數介於0~1)
(3) 在不重疊的時間段落裡，事件各自發生的次數是獨立的。(每一次$\Delta t$是獨立事件)

假設在T時間內發生k次事件的機率
由(1)(2)知 $P(1,\Delta t)=\lambda\Delta t$
且 $P(k,\Delta t)=0$, $k\geq 2$

現將 T 分割成 N 個短時間區段 （即 $T=N\Delta t$）
利用 (3) 各時間區段出現之事件是獨立的條件，可知

$P(k, T) ~ C^{N}_{k}(\lambda \Delta t)^{k}(1-\lambda\Delta t)^{N-k}$

$=\frac{N(N-1)...(N-k+1)}{k!}\lambda^k\frac{T^k}{N^k}\frac{(1-\frac{\lambda T}{N})^N}{(1-\frac{\lambda T}{N})^k}$

$=\frac{(\lambda T)^k}{k!}\frac{N(N-1)...(N-k+1)}{N N N...N}\frac{(1-\frac{\lambda T}{N})^N}{(1-\frac{\lambda T}{N})^k}$
固定 k，當 $N\rightarrow\infty$ 時

$P(X=k) = \frac{e^{-\lambda}\lambda^{k}}{k!}$

由上可知 Poisson 分配是二項分配 B(N,p,q) 的一種極限，其中 Np= 常數 $\lambda T$，再讓 $N\rightarrow\infty$
另外，我們通常將 $\lambda T$ 記為 m，表示在時間區間 T 中，平均的發生次數

http://episte.math.ntu.edu.tw/articles/sm/sm_16_07_1/index.html

Attacker追上交易的機率

讓我們回到剛剛想計算的, Attacker如果想追回已經確認的交易並做修改的機率要如何做計算?

這裡會將計算分成兩個部分

1. Attacker產生k個block的機率
2. Attacker產生k個block追上honest z個block的機率

首先honest blocks 我們假設大概是固定速率在增長
我們想要計算接收者在z個block以後確認交易的被攻擊的可能性(代表作弊者要追z個block)
假設p是honest 節點找到block的機率(算力比), q是attacker找到節點的機率
p + q = 1

Attacker 產生k個block追上honest z個block的機率

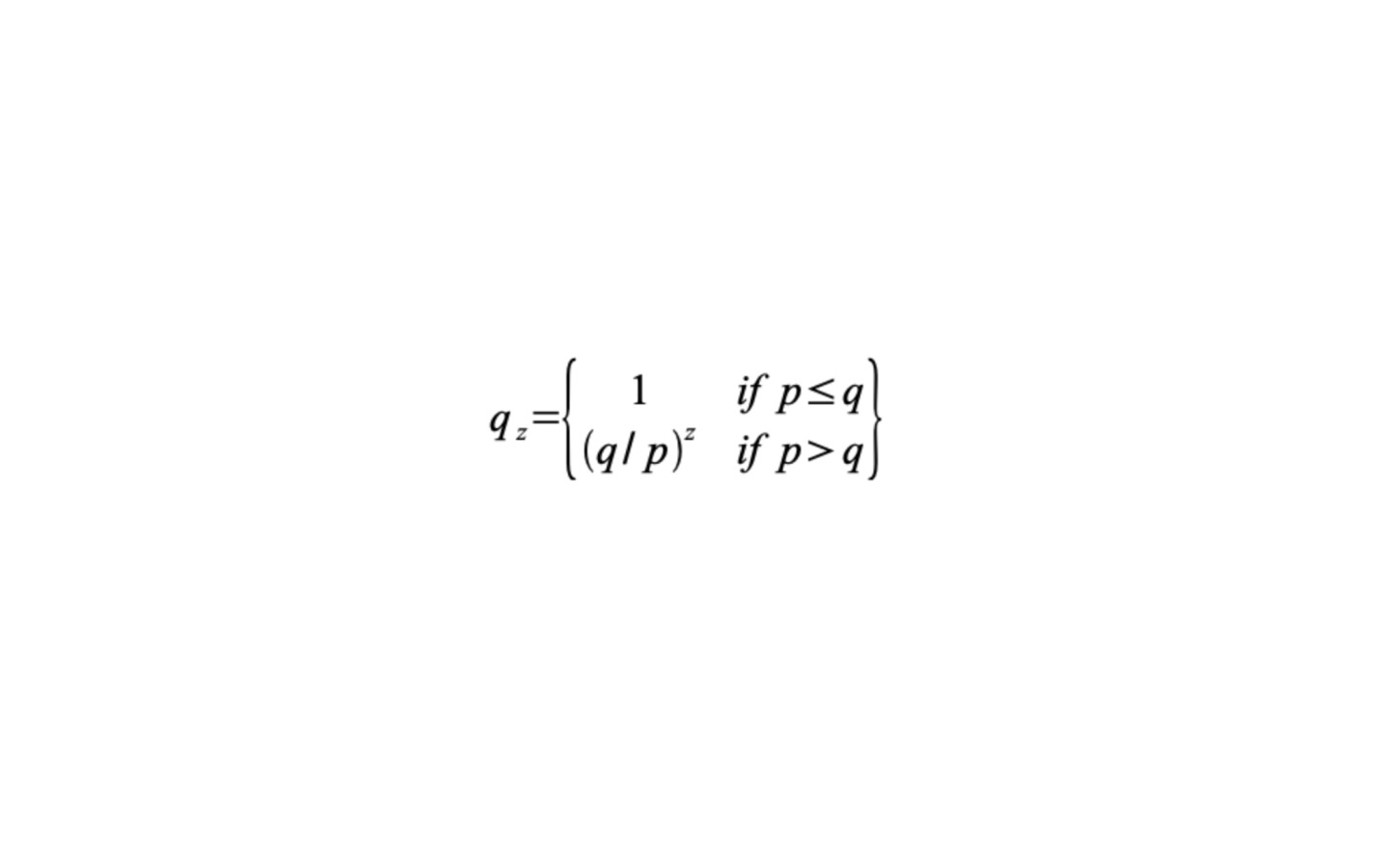
上面可以看到如果, attacker比honest快的話(q>p), 那麼要追上的機率是1
反之機率則呈現指數衰減

Attacker 產生k個block的機率

在honest產生z個區塊的時間, attacker會產生幾個block我們不確定, 但是應該是符合下面比例的
$\lambda = z\frac{q}{p}$

根據Possion distribution, 如果attacker在$\Delta t$中獎z個block的中獎機率為
$\frac{\lambda^ke^{-\lambda}}{k!}$

結合計算

由於k可能是在任何數字追上, 所以我們必須把任何可能的k累加起來, 就是最終k追上z的機率

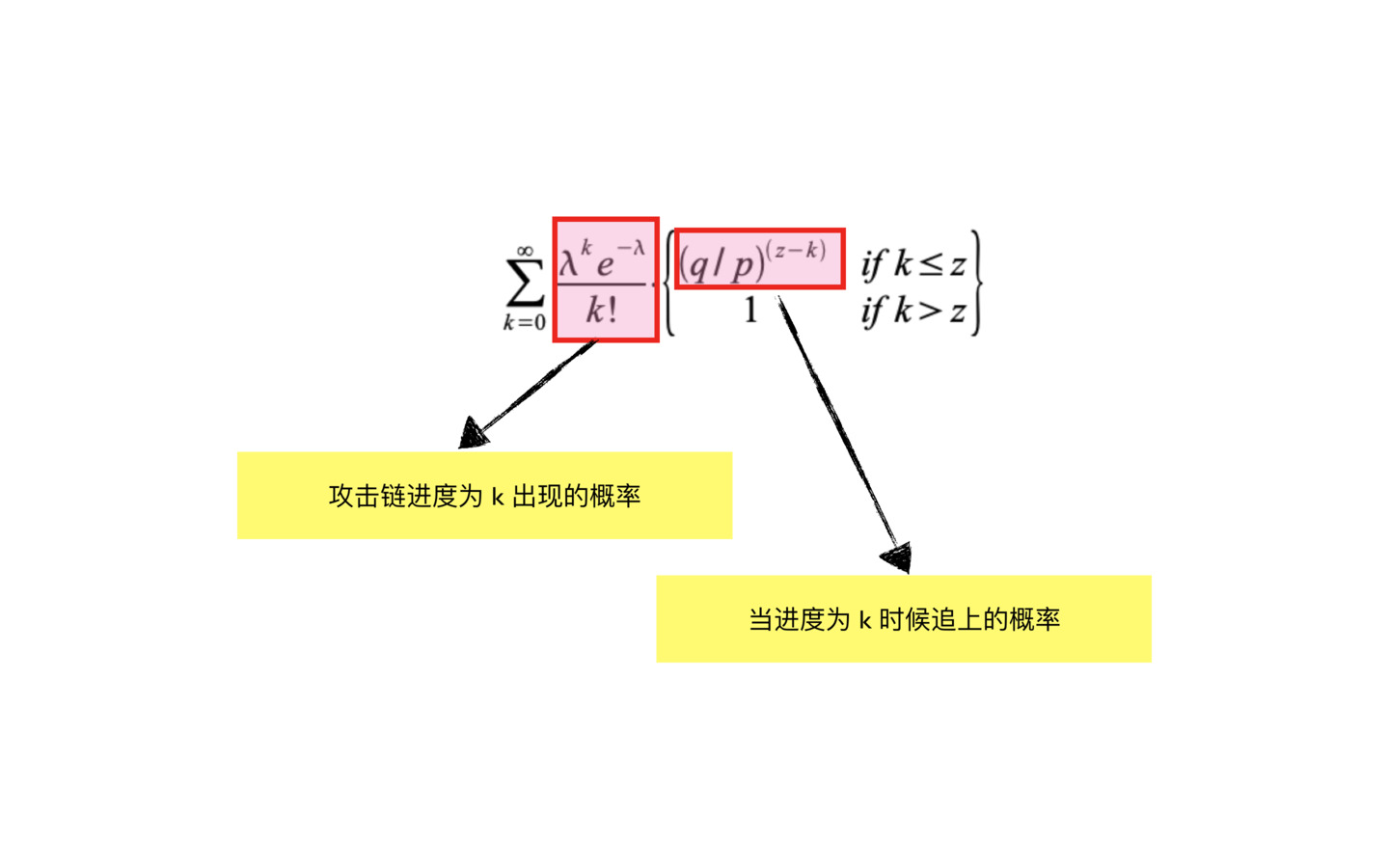
下面把公式變換一下, 我們把追上的機率轉換為追不上的機率, 再用1減去追不上的機率, 就是追上的機率

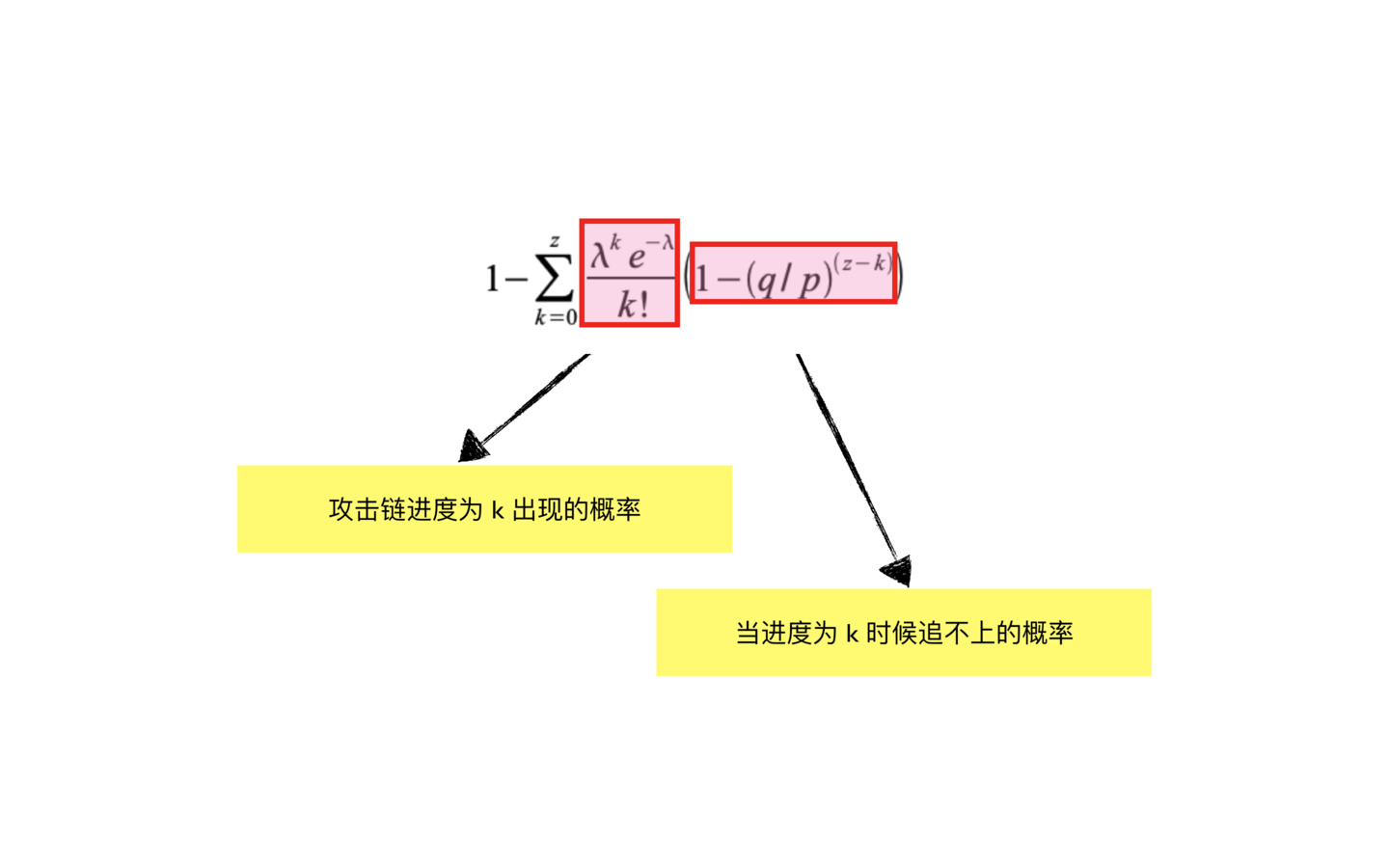
當k 大於z ，表示攻擊已經成功，已經追上了，所以也就不存在追不上的概率了，所以計算k 的取值範圍就是0 到z 了

下面是程式碼的實現

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
    double p = 1.0 - q;
    double lambda = z * (q / p);
    double sum = 1.0;
    int i, k;
    for (k = 0; k <= z; k++)
    {
        double poisson = exp(-lambda);
        for (i = 1; i <= k; i++)
            poisson *= lambda / i;
        sum -= poisson * (1 - pow(q / p, z - k));
    }
    return sum;
}

Solving for P less than 0.1%...
下面代表了如果attacker擁有的算力佔比多少, 至少需要多少個block才能確定交易無誤
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340

當然這一切的假設都是在於q < p
老實說攻擊者的攻擊成功的機率比我想像的還高, 只要佔全網1/10的算力, 在領先5個block情況下, 還有1/1000機率會被攻擊成功

如果喜歡文章, 不妨按下喜歡訂閱支持

如果真的想支持我進行創作與實踐計畫, 也可以進行打賞
BTC (BTC) : 1LFRBqvWR9GGizBzoFddkb5xRpAzKRVoDC
BTC (BSC) : 0xe1cda3eb778d1751af17feac796a4bbe4dbca815
BTC (ERC20) : 0xe1cda3eb778d1751af17feac796a4bbe4dbca815
USDT (TRC20) : TT7wgKuYoHwfRy3vCr38Qy3gnS3JJ1aKvn

如果想使用幣安, 可以使用我的推薦連結可以節省手續費10%
或使用推薦碼 : A5YRMD2T